Disposizione dei cavi dei ponti sospesi
La costruzione di un ponte, problema che per la sua utilità ha suscitato interesse fin dall’antichità, richiede, in alcuni casi, l’impiego di un’elevata tecnologia e spesso la soluzione trovata è stata perfezionata solo in tempi successivi. Fra i ponti con luci libere più grandi, i più imponenti sono sicuramente i ponti sospesi, ponti cioè in cui l’impalcato è sospeso mediante tiranti in acciaio ai cavi portanti disposti secondo una certa curva e sostenuti da alti piloni.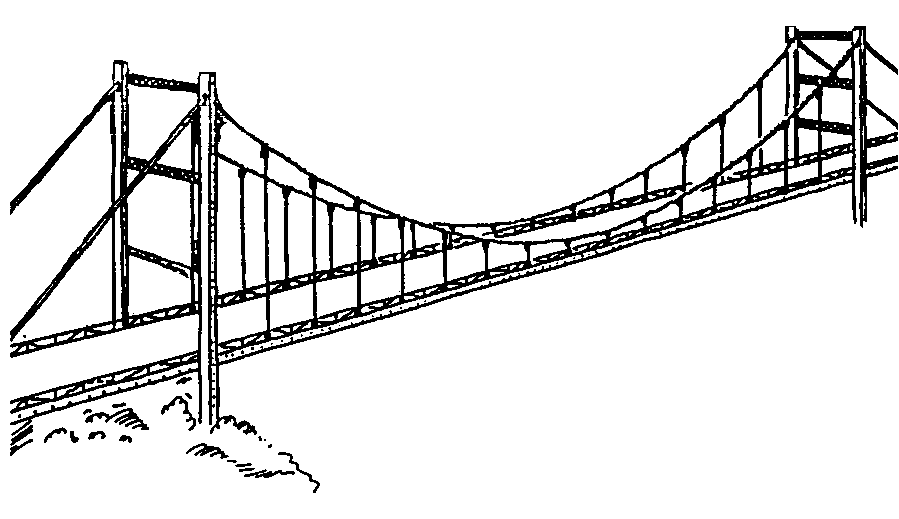 |
Il Golden Gate, sulla baia di S. Francisco, è uno dei ponti maggiori di questo tipo; è stato costruito negli anni ’30 ed ha una luce libera di 1280 m. Quello che forse non tutti immaginano è che i cavi d’acciaio del Golden Gate hanno 93 cm di diametro e sono formati da 27500 "fili" di 6 mm di diametro, pesano da soli circa 15.000 tonnellate e sostengono un impalcato a 75 m dal mare. Le torri sono alte 223 m sopra il pelo dell’acqua. Questi dati possono forse aiutare a capire l’interesse non solamente matematico per calcolare la "certa curva" lungo cui si dispongono i cavi in modo da conoscere la lunghezza dei tiranti prima di aver iniziato la costruzione del ponte. La curva che si ottiene fissando per i due estremi una fune senza alcun peso si chiama catenaria e a prima vista potrebbe sembrare la curva lungo cui si dispongono i cavi del nostro ponte. In realtà tenendo conto delle forze che agiscono sui cavi a causa del peso dell’impalcato dimostreremo come questi si dispongono lungo curve paraboliche. Per facilitare il nostro ragionamento schematizziamo la situazione considerando l’impalcato come un’asta rigida e formuliamo le seguenti ipotesi:
- i tiranti sono in numero pari e sono equispaziati (chiamiamo a la distanza lungo l’impalcato fra due tiranti consecutivi),
- cavi e tiranti sono perfettamente flessibili e inestensibili,
- il ponte è simmetrico rispetto alla retta perpendicolare all’impalcato che passa per il suo punto di mezzo.
Fissiamo allora un sistema di riferimento con l’asse delle x e quello delle y coincidenti rispettivamente con l’impalcato e con l’asse di simmetria. In questo modo basterà considerare i punti di ascissa positiva.
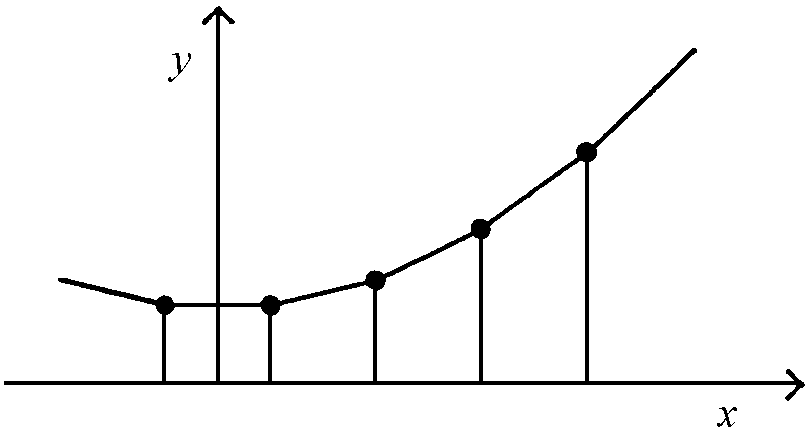 |
xk = (k - 1/2) a con k = 1, ...n
Per calcolare yk dobbiamo imporre sul punto Pk la condizione di equilibrio statico e per questo consideriamo le varie forze che agiscono su un vertice della spezzata ovvero: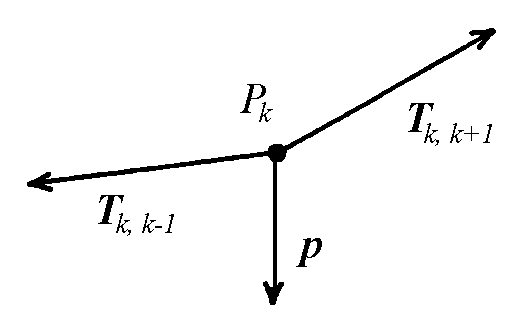 |
- la forza peso p diretta lungo l’asse y di intensità uguale per ogni k in quanto il peso totale è equamente distribuito su ciascun tirante,
- la tensione Tk,k-1 diretta lungo il segmento Pk Pk-1
- la tensione Tk,k+1 diretta lungo il segmento Pk Pk+1
- (Tk,k-1)x = (Tk,k+1)x [lungo l’asse x]
- (Tk,k-1)y + p= (Tk,k+1)y [lungo l’asse y]
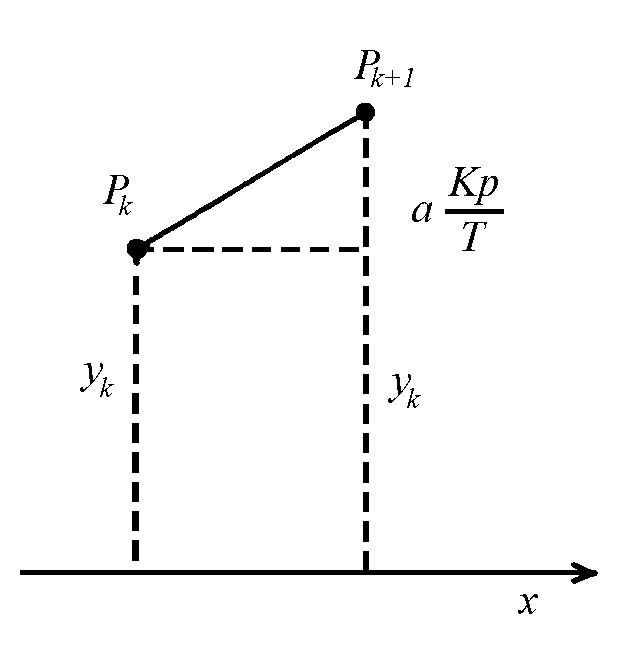 |
| (Tk,k-1)x| = | (T1,0)x| = T
| (Tk,k-1)y| = k | p | = kp Poiché yk+1 = yk + a kp/T con k = 1, ...n possiamo scrivere: yk+1 = yk + a kp/T = yk-1 + a(k-1)p/T + a kp/T = y1 + ap (1+2+...+k)/T = b + [akp (k+1)/2T] Così le coordinate del punto Pk sono:
xk = (k-1/2)a
yk = b + [akp (k-1)/2T]
con k = 1, ...,n
ovvero i vertici della nostra spezzata appartengono alla parabola di equazione:y = (p/2aT) x2 + (b - ap/8T)